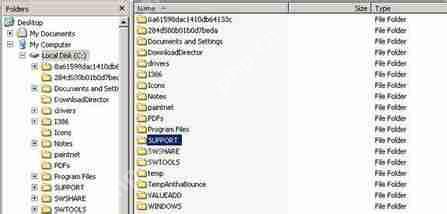
前面所討論的線性表元素之間都是一對一的關(guān)系,今天我們所看到的結(jié)構(gòu)各元素之間卻是一對多的關(guān)系。樹在計算機中有著廣泛的應(yīng)用,甚至在計算機的日常使用中,也可以看到樹形結(jié)構(gòu)的身影,如下圖所示的windows資源管理器和應(yīng)用程序的菜單都屬于樹形結(jié)構(gòu)。樹形結(jié)構(gòu)是一種典型的非線性結(jié)構(gòu),除了用于表示相鄰關(guān)系外,還可以表示層次關(guān)系。本文重點討論樹與二叉樹的基本結(jié)構(gòu)和遍歷算法等內(nèi)容。
一、好大一棵樹,綠色的祝福1.1 樹的基本概念
1.2 樹的基本術(shù)語
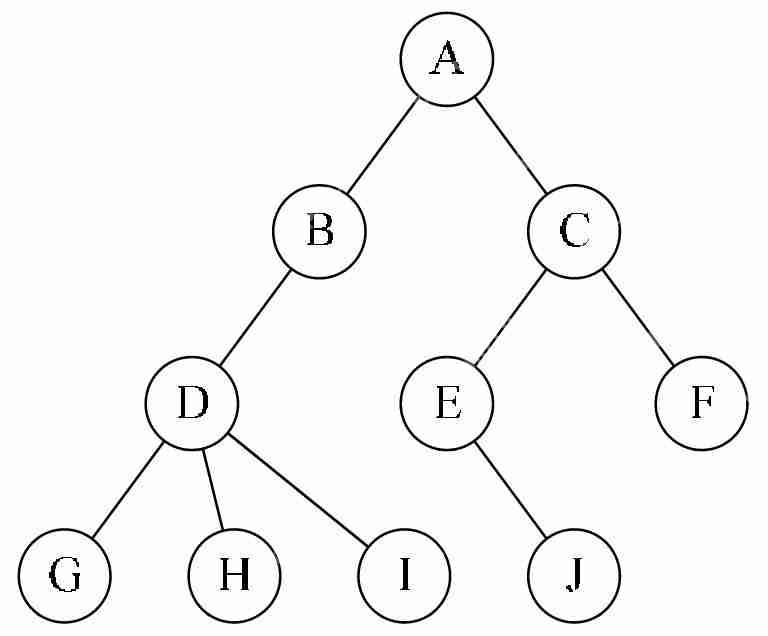
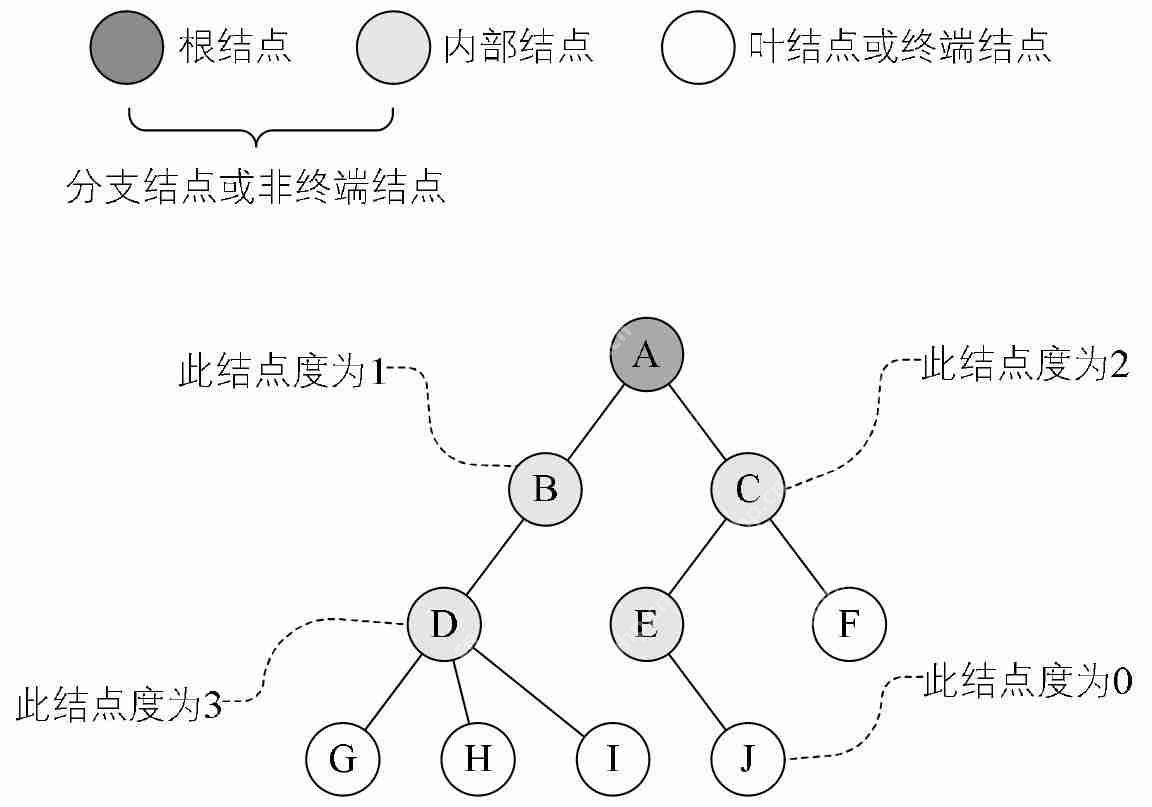
(1)不同的節(jié)點:根節(jié)點、內(nèi)部節(jié)點、葉子節(jié)點以及節(jié)點的度
(2)節(jié)點的關(guān)系:雙親與孩子,爸爸回來了,爸爸去哪兒?
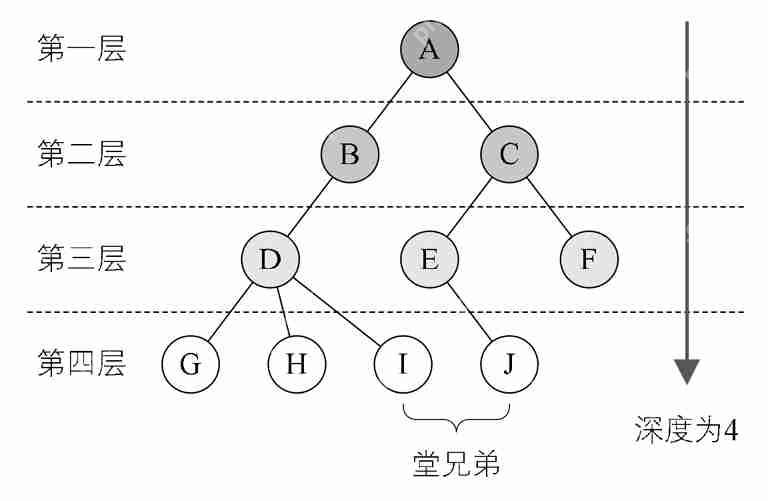
(3)節(jié)點的層次:結(jié)點的層次(Level)從根開始定義起,根為第一層,根的孩子為第二層。樹中結(jié)點的最大層次稱為樹的深度(Depth)或高度。
二、二叉樹又是個什么鬼2.1 從猜數(shù)字游戲引出二叉樹
回憶一下,當年某電視節(jié)目中會讓游戲參與者猜一個產(chǎn)品的價格,如果參與者在限定時間內(nèi)猜對了,那么他就可以獲得這個產(chǎn)品。很多人都是一點點的提高數(shù)值來猜,但是這樣猜會很沒有效率。因此,很多聰明人都知道需要利用折半查找的思想去猜測。假定某個產(chǎn)品在100元的范圍內(nèi),那么可以在7次之內(nèi)猜出結(jié)果來,如下圖所示:(由于是100以內(nèi)的正整數(shù),所以我們先猜50(100的一半),被告之“大了”,于是再猜25(50的一半),被告之“小了”,再猜37(25與50的中間數(shù)),小了,于是猜43,大了,40,大了,38,小了,39,完全正確。)
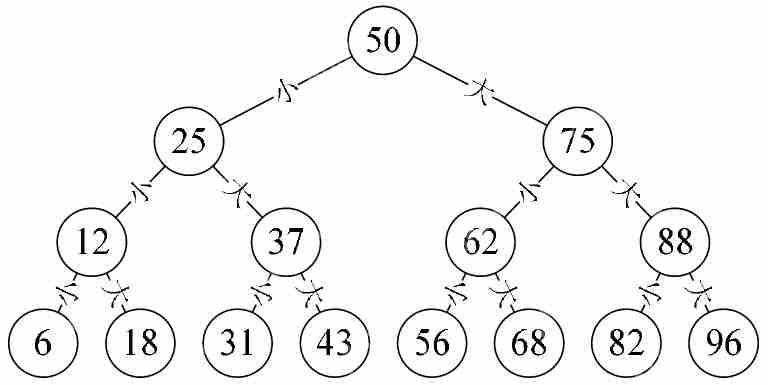
如上圖所示,對于這種在某個階段都是兩種結(jié)果的情形,比如開和關(guān)、0和1、真和假、上和下、對與錯,正面與反面等,都適合用樹狀結(jié)構(gòu)來建模,而這種樹是一種很特殊的樹狀結(jié)構(gòu),叫做二叉樹。
2.2 二叉樹的順序存儲結(jié)構(gòu)
二叉樹的順序存儲結(jié)構(gòu)就是用一維數(shù)組存儲二叉樹中的結(jié)點。結(jié)點的存儲位置,也就是數(shù)組的下標要能體現(xiàn)結(jié)點之間的邏輯關(guān)系,比如雙親與孩子的關(guān)系,左右兄弟的關(guān)系等。
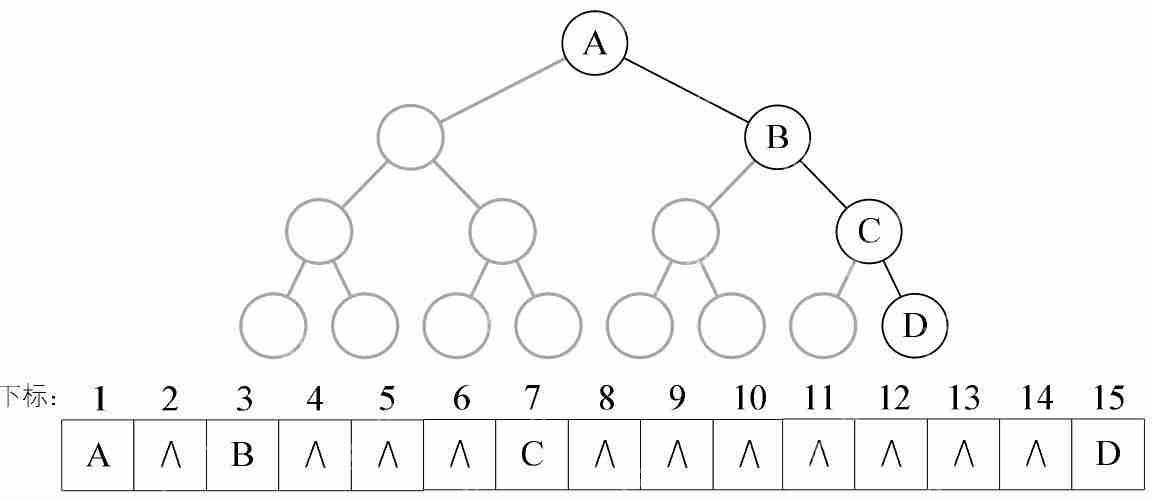
But,考慮一種極端的情況,一棵深度為k的右斜樹,它只有k個結(jié)點,卻需要分配2的k次方-1個存儲單元空間,這顯然是對存儲空間的浪費,所以,順序存儲結(jié)構(gòu)一般只適用于完全二叉樹。
2.3 二叉樹的鏈式存儲結(jié)構(gòu)
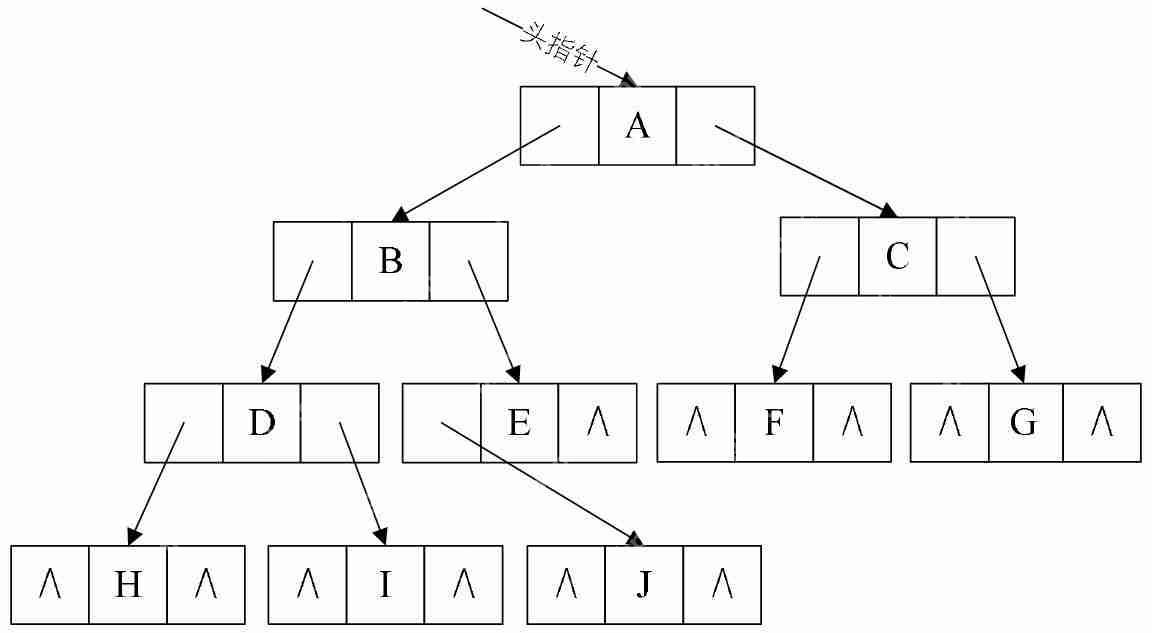
既然順序存儲適用性不強,我們就要考慮鏈式存儲結(jié)構(gòu)。二叉樹每個結(jié)點最多有兩個孩子,所以為它設(shè)計一個數(shù)據(jù)域和兩個指針域是比較自然的想法,我們稱這樣的鏈表叫做二叉鏈表。其中data是數(shù)據(jù)域,lchild和rchild都是指針域,分別存放指向左孩子和右孩子的指針。
三、二叉樹的代碼實現(xiàn)3.1 二叉樹的C#代碼實現(xiàn)
(1)二叉樹節(jié)點的定義:
代碼語言:JavaScript代碼運行次數(shù):0運行復(fù)制
/// <summary> /// 二叉樹的節(jié)點定義 /// </summary> /// <typeparam name="T">數(shù)據(jù)具體類型</typeparam> public class Node<t> { public T data { get; set; } public Node<t> lchild { get; set; } public Node<t> rchild { get; set; } public Node() { } public Node(T data) { this.data = data; } public Node(T data, Node<t> lchild, Node<t> rchild) { this.data = data; this.lchild = lchild; this.rchild = rchild; } }</t></t></t></t></t>
(2)二叉樹的創(chuàng)建實現(xiàn):
代碼語言:javascript代碼運行次數(shù):0運行復(fù)制
// Method01:判斷該二叉樹是否是空樹 public bool IsEmpty() { return this.root == null; } // Method02:在節(jié)點p下插入左孩子節(jié)點的data public void InsertLeft(Node<t> p, T data) { Node<t> tempNode = new Node<t>(data); tempNode.lchild = p.lchild; p.lchild = tempNode; } // Method03:在節(jié)點p下插入右孩子節(jié)點的data public void InsertRight(Node<t> p, T data) { Node<t> tempNode = new Node<t>(data); tempNode.rchild = p.rchild; p.rchild = tempNode; } // Method04:刪除節(jié)點p下的左子樹 public Node<t> RemoveLeft(Node<t> p) { if (p == null || p.lchild == null) { return null; } Node<t> tempNode = p.lchild; p.lchild = null; return tempNode; } // Method05:刪除節(jié)點p下的右子樹 public Node<t> RemoveRight(Node<t> p) { if (p == null || p.rchild == null) { return null; } Node<t> tempNode = p.rchild; p.rchild = null; return tempNode; }</t></t></t></t></t></t></t></t></t></t></t></t>
以上四個方法分別提供了新節(jié)點的插入以及移除的實現(xiàn),我們可以針對某個節(jié)點進行插入左孩子有右孩子節(jié)點。
(3)二叉樹的遞歸遍歷:
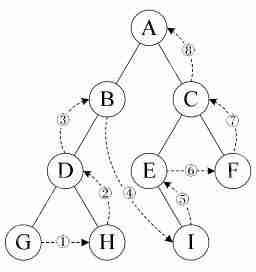
首先我們通過幾張圖來看看二叉樹的三種基本遍歷:前序、中序以及后序遍歷;
①前序遍歷:若根節(jié)點不為空,則先訪問根節(jié)點,然后先序遍歷左子樹,最后先序遍歷右子樹;

②中序遍歷:若根節(jié)點不為空,則先中序遍歷左子樹,再訪問根節(jié)點,最后中序遍歷右子樹;

③后序遍歷:若根節(jié)點不為空,則首先后序遍歷左子樹,其次后序遍歷右子樹,最后訪問根節(jié)點;
代碼語言:javascript代碼運行次數(shù):0運行復(fù)制
// Method01:前序遍歷 public void PreOrder(Node<t> node) { if (node != null) { // 根->左->右 Console.Write(node.data + " "); PreOrder(node.lchild); PreOrder(node.rchild); } } // Method02:中序遍歷 public void MidOrder(Node<t> node) { if (node != null) { // 左->根->右 MidOrder(node.lchild); Console.Write(node.data + " "); MidOrder(node.rchild); } } // Method03:后序遍歷 public void PostOrder(Node<t> node) { if (node != null) { // 左->右->根 PostOrder(node.lchild); PostOrder(node.rchild); Console.Write(node.data + " "); } } </t></t></t>
本次實現(xiàn)采用了遞歸的方式實現(xiàn)遍歷算法,主要是根據(jù)二叉樹三種遍歷(前序、中序以及后序遍歷)的要求,依次輸出各個節(jié)點的元素。至于非遞歸方式的遍歷算法以及層次遍歷算法會在下一篇中進行介紹。
3.2 測試二叉樹的遍歷方法
在上面的代碼中,我們實現(xiàn)了二叉樹的遞歸遍歷算法,這里我們通過一段簡單的測試代碼來構(gòu)造一顆二叉樹,并進行遍歷。首先,通過下圖看看我們要創(chuàng)建的一顆二叉樹是什么鬼?
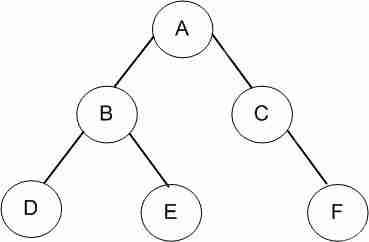
(1)測試代碼:
代碼語言:javascript代碼運行次數(shù):0運行復(fù)制
static void MyBinaryTreeBasicTest() { // 構(gòu)造一顆二叉樹,根節(jié)點為"A" MyBinaryTree<string> bTree = new MyBinaryTree<string>("A"); Node<string> rootNode = bTree.Root; // 向根節(jié)點"A"插入左孩子節(jié)點"B"和右孩子節(jié)點"C" bTree.InsertLeft(rootNode, "B"); bTree.InsertRight(rootNode, "C"); // 向節(jié)點"B"插入左孩子節(jié)點"D"和右孩子節(jié)點"E" Node<string> nodeB = rootNode.lchild; bTree.InsertLeft(nodeB, "D"); bTree.InsertRight(nodeB, "E"); // 向節(jié)點"C"插入右孩子節(jié)點"F" Node<string> nodeC = rootNode.rchild; bTree.InsertRight(nodeC, "F"); // 前序遍歷 Console.WriteLine("---------PreOrder---------"); bTree.PreOrder(bTree.Root); // 中序遍歷 Console.WriteLine(); Console.WriteLine("---------MidOrder---------"); bTree.MidOrder(bTree.Root); // 后序遍歷 Console.WriteLine(); Console.WriteLine("---------PostOrder---------"); bTree.PostOrder(bTree.Root); }</string></string></string></string></string>
(2)運行結(jié)果:
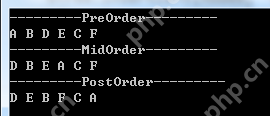
附件下載
本文實現(xiàn)的C#版二叉樹參考代碼下載:http://pan.baidu.com/s/1eQ1xmXs
參考資料
(1)程杰,《大話數(shù)據(jù)結(jié)構(gòu)》
(2)陳廣,《數(shù)據(jù)結(jié)構(gòu)(C#語言描述)》
(3)段恩澤,《數(shù)據(jù)結(jié)構(gòu)(C#語言版)》
(4)楊俊明,《數(shù)據(jù)結(jié)構(gòu)C#版筆記—樹與二叉樹》
(5)Frank Fan,《萬丈高樓平地起之C#實現(xiàn)二叉樹操作》
作者:周旭龍
出處:http://edisonchou.cnblogs.com
本文版權(quán)歸作者和博客園共有,歡迎轉(zhuǎn)載,但未經(jīng)作者同意必須保留此段聲明,且在文章頁面明顯位置給出原文鏈接。







