以下是對給定文章進行偽原創的輸出,確保不改變文章的大意和圖片的位置,并保持原文的語言:
- 字典字符集的笛卡爾乘積
問題描述:對于一個由字典字符集組合而成的表達式,如何求出所有可能的元素組合?例如,表達式[0-9][a-z],其中0-9代表10個數字,a-z代表26個小寫字母,其所有可能的元素組合為0a, 0b, …, 0z, 1a, 1b, …, 9z。字典字符集的笛卡爾乘積示例如下:
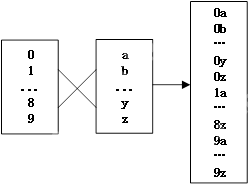
問題分析:對于任意一個由字典字符集構成的表達式[dic0][dic1]…[dicn],可以將其從左到右視為一個由字典元素組成的“數”,這符合我們日常表示數值的高低位習慣。例如,如果所有字典都是[0-9],那么表達式[0-9][0-9]就代表數值字符串00到99。笛卡爾乘積的空間是各個字典高度的乘積,給定其空間中的任意一個元素下標,就可以對應到每個字典中的元素下標。比如[0-9][0-9]的笛卡爾乘積空間是10*10=100,第0個元素是00,第99個元素是99。
每個字典元素都有一個位權重。例如,表達式[0-9][0-9]中,第一個字典的位權重w=10,第二個字典的位權重w=1。我們常說的個位、十位、百位,就是基于數值位的位權重來稱呼的。位權重的意義在于,數值是其位權重的多少倍,就取第幾個元素。例如,第99個元素(下標從0開始),數值99是十位的位權重w=10的9倍,所以元素為字符‘9’,對數值99取w=10的余數得9,9是個位的位權重w=1的9倍,所以元素為字符‘9’,因此構成了字符串99。
實現示例:對于表達式[0-9][a-z][A-Z],其笛卡爾乘積的具體過程可以描述如下:(1)從左至右(高位到低位)計算各個字典字符集所在數位的計算單位,通過當前字典右邊的字典高度相乘得到,例如[0-9]的計數單位w=2626=676,[a-z]的計數單位w=261=26,[A-Z]的計數單位w=1。(2)給定笛卡爾乘積空間的元素下標i,根據i找到各個字典內的元素下標的過程如下,從高位開始查找,即從左開始查找。(2.1)查找字典[0-9]中的元素下標:[0-9].index=i/[0-9].w;(2.2)查找字典[a-z]中的元素下標[a-z].index:i=i%[0-9].w; [a-z].index=i/[a-z].w;(2.3)查找字典[A-Z]中的元素下標[A-Z].index:i=i%[a-z].w;[A-Z].index=i/1=i。(3)將i從0遞增至笛卡爾乘積的空間大小減一,即10*26*26-1,重復步驟2,即可完成表達式[0-9][a-z][A-Z]的笛卡爾乘積。
例如,給定第677個笛卡爾乘積的元素,那么[0-9].index=1,所以取[0-9]內的元素‘1’,[a-z].index=671%676/26=0,所以取出元素‘a’,[A-Z].index=1/1=1,所以取出元素‘B’,因此第677個元素就是“1aB”。
- 源碼
以下代碼在Linux平臺上編譯運行,稍作修改即可移植到Windows平臺。其功能是完成多個字典字符集的笛卡爾乘積,并通過OpenMP進行并行加速。該代碼的正確性已在實際項目中通過驗證。
代碼語言:JavaScript 代碼運行次數:0
運行 復制
#include <pthread.h> #include <omp.h> #include <iostream> #include <map> #include <string> using namespace std; typedef unsigned char uint8; <p>// 字典字符集與段字符集 struct charset_mem{ int high, width; // 字符集的寬度和高度 int mem_size; // 字符集data所占用的內存,單位字節 uint8 *data; // 字符集的數據 char name[128]; // 字符集名稱 };</p><p>map<string> dic_utf8_charset_map; // 全局字典字符集緩存 map<string> dic_ucs2_charset_map; // 全局字典字符集緩存 map<string> seg_charset_map; // 全局段字符集緩存 pthread_mutex_t charset_mutex;</p><p>// 功能:根據多個字典字符集生成相應的笛卡爾乘積 // 參數:charsetID:笛卡爾乘積結果字符集名稱,dicNum:字典字符集數目,dicName:字典字符集名稱數組指針,encode:字典字符編碼類型 // 返回值:成功返回true,失敗返回false bool cartesianProduct(string charsetID, int dicNum, char(<em>dicName)[128], uint8 encode){ pthread_mutex_lock(&charset_mutex); // 對字符集的map關聯容器修改需要加鎖 string charsetNewedID = charsetID; map<string>::iterator iter; charset_mem</em> segNewedCharset = new charset_mem; memset(segNewedCharset, 0, sizeof(charset_mem)); strcpy(segNewedCharset->name, charsetNewedID.c_str());</p><pre class="brush:php;toolbar:false">#define MAX_WORD_LEN 40 #define MAX_DIC_NUM 32 // 笛卡爾乘積(cartesian product)準備工作 map<string>& dic_charset_map = (0 == encode) ? dic_utf8_charset_map : dic_ucs2_charset_map; int high = 1, width = 0; int s[MAX_DIC_NUM] = {0}; // 字典段進制位 for(int i = dicNum - 1; i >= 0; --i){ iter = dic_charset_map.find(dicName[i]); s[i] = iter->second->high; high *= iter->second->high; width += iter->second->width; } segNewedCharset->high = high; segNewedCharset->width = width; segNewedCharset->data = new uint8[high * width]; // 笛卡爾乘積 int thread_num = omp_get_max_threads(); // 獲取處理器最大可并行的線程數 #pragma omp parallel for num_threads(thread_num) for(int i = 0; i < high; ++i){ uint8 wordTmp[MAX_WORD_LEN] = {0}; map<string>::iterator iterTmp; int offset = 0; int charpos = i; for(int j = 0; j < dicNum; ++j){ iterTmp = dic_charset_map.find(dicName[j]); int indexDic = charpos / s[j]; int offsetDic = indexDic * iterTmp->second->width; memcpy(wordTmp + offset, iterTmp->second->data + offsetDic, iterTmp->second->width); charpos = charpos % s[j]; offset += iterTmp->second->width; } memcpy(segNewedCharset->data + i * segNewedCharset->width, wordTmp, segNewedCharset->width); } // 將結果字符集添加到,map映射表 seg_charset_map.insert(pair<string>(charsetNewedID, segNewedCharset)); pthread_mutex_unlock(&charset_mutex); return true;
}
- 優化
在撰寫畢業論文時,通過實驗室同學的建議,發現無需預先計算各個字典所在數位的計數單位,也可以根據給定的笛卡爾乘積的元素下標唯一地找到各個字典中對應的元素。為了避免論文查重時的重復,這里只展示圖片。具體實現已經抽象為以下算法:

算法中的注釋中的熱詞就是上文提到的字典,其實現原理是從表達式的低位到高位計算每一個字典的元素下標,而未優化的方法是從高位到低位順序計算。從低位到高位計算時,無需預先求出各個字典位的計數單位。因為:當字典位的計數單位為w=1時,可以通過笛卡爾乘積的元素下標i對其高度h取余,即得到最低字典位字典內的元素下標。當對下一個字典求其元素下標時,需要將下一個字典位的計數單位w’變為1,具體做法就是i除以當前字典的高度向下取整。依次類推,就可以求出各個字典內的元素下標了。具體描述見上面的算法。
以表達式[0-9][a-z][A-Z]為例,求笛卡爾乘積中第677個(從0開始)元素的各個字典內的元素下標的過程描述如下:(1)求字典[A-Z]的元素下標index=i%[A-Z].h=677%26=1,所以取元素‘B’;(2)求字典[a-z]的元素下標index:(2.1)將[a-z]的計數單位變為1,做法是i=i/[A-Z].h=677/26=26;(2.2)求[a-z].index=i%[a-z].h=26%26=0,所以取元素‘a’。(3)求字典[0-9]的元素下標index:(3.1)將[0-9]的計數單位變為1,做法是i=i/[a-z].h=26/26=1;(3.2)求[0-9].index=i%[0-9].h=1%10=1,所以取元素‘1’。因此,第677個笛卡爾乘積的元素就是“1aB”,與上面的算法殊途同歸。
- 再優化
仔細閱讀上面的算法描述,你會發現算法的內層循環存在重復的字典元素拷貝,例如笛卡爾乘積元素下標0~25對應的字典[0-9]和[a-z]內的元素下標始終是0,那么就重復拷貝了[0-9]和[a-z]中元素25次。針對該問題,可以對上面的算法做進一步的優化。
以一次字典元素拷貝作為基本操作,那么第二小節和第三小節的時間復雜度是O(hn),h為笛卡爾乘積空間大小,n為字典個數。
再優化算法描述如下:

再優化步驟描述如下:(1)選取高度最高的字典S_k;(2)循環h次,h為其它字典高度的乘積;(2.1)將其它字典元素拼接在一起;(2.2)循環最高字典高度H_k次,k為最高字典的下標,將元素填充到臨時字符串s中后,將s加入笛卡爾乘積集合。
時間復雜度為O(h_0(n-1)+h_0h_1)=O(h_0(h_1+n-1))。其中h_0為非最高字典高度乘積,h_1為最高字典高度,n為字典個數,n≥2。上文中未優化的時間復雜度是優化后的倍數t=h_0h_1n/h_0(h_1+n-1)=n/(1+(n-1)/ h_1),可見,n和h_1越大,優化效果越明顯。假設h_1*很大,那么優化的倍數大約為字典的個數。