?

哈希函數(shù)(Hash function)為根據(jù)索引鍵來返回數(shù)值哈希程序代碼的算法。索引鍵(Key)是被存儲對象的某些屬性值(Value)。當對象加入至 Hashtable時，它存儲在與對象哈希程序代碼相符的哈希程序代碼相關的Bucket中。當在Hashtable內搜尋值時，哈希程序代碼會為該值產(chǎn)生，并且會搜尋與該哈希程序代碼相關的Bucket。例如，student和teacher會放在不同的Bucket中，而dog和god會放在相同的 Bucket中。所以當索引鍵是唯一從Hashtable獲取元素的性能時表現(xiàn)會較好。Hash的四大優(yōu)點如下所示。

· 事先不需要排序。

· 搜尋速度與數(shù)據(jù)多少無關。

· 數(shù)字簽名的密碼技術保密性(Security)高。

· 可做數(shù)據(jù)壓縮(Data Compression)，以節(jié)省空間。

Linux內核里的哈希表應用非常廣泛，php內核里大部分語言特性也是基于哈希表實現(xiàn)的。為什么哈希表能這么神通廣大?哈希表能夠實現(xiàn)高效的數(shù)據(jù)存儲和查找，而存儲和查找是編程中應用最廣泛的兩個操作。

讀過Linux內核源碼的人可能都會發(fā)現(xiàn)，其中并沒有太多復雜的數(shù)據(jù)結構，作為基礎數(shù)據(jù)結構的雙向鏈表(list)和基于list實現(xiàn)的hash表占據(jù)了絕大部分數(shù)據(jù)結構。內核為什么會大量使用這兩種數(shù)據(jù)結構呢?
首先，這兩種數(shù)據(jù)結構都十分簡單，簡單包括理解起來簡單和使用起來簡單兩方面內容。這也意味著代碼的可讀性和可維護性都比其他復雜的數(shù)據(jù)結構要好，出現(xiàn)bug的風險也較低。從哲學上來講，這也符合K.I.S.S.條款。

其次，內核是一個比較講究性能的軟件，為了程序設計和維護的簡單性而失掉性能，這究竟是不是算得不償失呢?我們是不是應該將天平更加偏向于性能?已經(jīng)記不起是在哪里聽說過，很多商業(yè)的路由軟件都是基于二叉樹的數(shù)據(jù)結構來存儲路由項，以求得其路由查找的時間復雜度為log(n)，并且他批評Linux的路由項組織為hash表，致使性能不佳，不適合商業(yè)。確實有一定道理，可仔細分析，hash表的性能真的比二叉樹差么?二叉樹的插入和刪除某一項的時間復雜度都為log(n);hash表插入和刪除的時間復雜度最好為O(1)，最差為O(n)，如果選取的表項(m)足夠多，且hash函數(shù)足夠好的話，其時間復雜度為O(n/m)(當m n / log(n)的時候，hash表的平均表現(xiàn)就比二叉樹要好;且當m>=n時，其時間復雜度趨近于O(1)。m的值可以做成可調整的，這也正顯示了內核的可定制性。不過，不要盲目樂觀，這一切都是以一個足夠好的hash函數(shù)為前期的。

如何判定一個hash函數(shù)的好壞呢?
hash的中文意思是“散列”，可解釋為：分散排列。一個好的hash函數(shù)應該做到對所有元素平均分散排列，盡量避免或者降低他們之間的沖突(Collision)。有必要再次提醒大家的是，hash函數(shù)的選擇必須慎重，如果不幸所有的元素之間都產(chǎn)生了沖突，那么hash表將退化為鏈表，其性能會大打折扣，時間復雜度迅速降為O(n)，絕對不要存在任何僥幸心理，因為那是相當危險的。歷史上就出現(xiàn)過利用Linux內核hash函數(shù)的漏洞，成功構造出大量使hash表發(fā)生碰撞的元素，導致系統(tǒng)被DoS，所以目前內核的大部分hash函數(shù)都有一個隨機數(shù)作為參數(shù)進行摻雜，以使其最后的值不能或者是不易被預測。這又對 hash函數(shù)提出了第二點安全方面的要求：hash函數(shù)最好是單向的，并且要用隨機數(shù)進行摻雜。提到單向，你也許會想到單向散列函數(shù)md4和md5，很不幸地告訴你，他們是不適合的，因為hash函數(shù)需要有相當好的性能。
Linux內核里面用的jhash是一個久經(jīng)考驗，并被實踐證明經(jīng)得起考驗的hash函數(shù)，可以CPMS(copy Paste Modify Save)之。Jhash的作者Bob jenkins在其網(wǎng)站上還公布了諸如針對能預知的數(shù)據(jù)進行hash的hash函數(shù)–完美(perfect)hash函數(shù)等一系列其他hash函數(shù)。
bucket的英文解釋：
Hash table lookup operations are often O(n/m) (where n is the number of objects in the table and m is the number of buckets), which is close to O(1), especially when the hash function has spread the hashed objects evenly through the hash table, and there are more hash buckets than objects to be stored.

可以這樣理解：

· 一個HASH的結果所對應的地址可存放兩個BUCKET。可解決HASH沖突。

· 要存數(shù)據(jù)時，第一次HASH到這里，在第一個BUCKET存放一個數(shù)據(jù)。

· 要存數(shù)據(jù)時，當?shù)诙我蚰承┰騂ASH到這里時，在第二個BUCKET存放另一個數(shù)據(jù)。

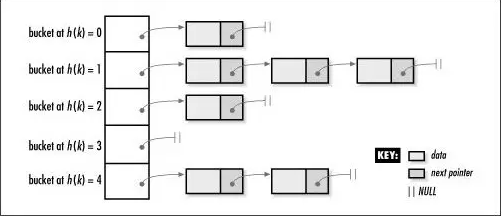
一個由5個buckets組成的哈希表，里面有7個元素：

linux的hash函數(shù)hash_long等，用了golden ratio來計算。因為桶(bits)的數(shù)量需要由hash函數(shù)和對沖突的期望來決定，那么對于hash_long這樣的hash函數(shù)，我們怎么確定桶的數(shù)量呢？
一般情況下都是自己根據(jù)數(shù)據(jù)特性來考慮使用的 hash 算法，不是千篇一律咬死一個不放，比如存放 IP 地址的 hash table，用一個 65536 的桶就很好，把 IP 的后 16bit 作為 key。這種方法絕對比 hash_long、jhash 等函數(shù)的碰撞率低。
其實就是這個界和性能的折中。我可以取我問題空間的最大值。這樣肯定能保證鍵值分散。但是這樣會浪費很多空間。然而取得太小，又影響查找效率。感覺還是要在試驗中進行測試。而且hash比其他搜索的數(shù)據(jù)結構靈活的地方就是它的可定制性。可以根據(jù)具體情況調整，以達到最優(yōu)的效果。